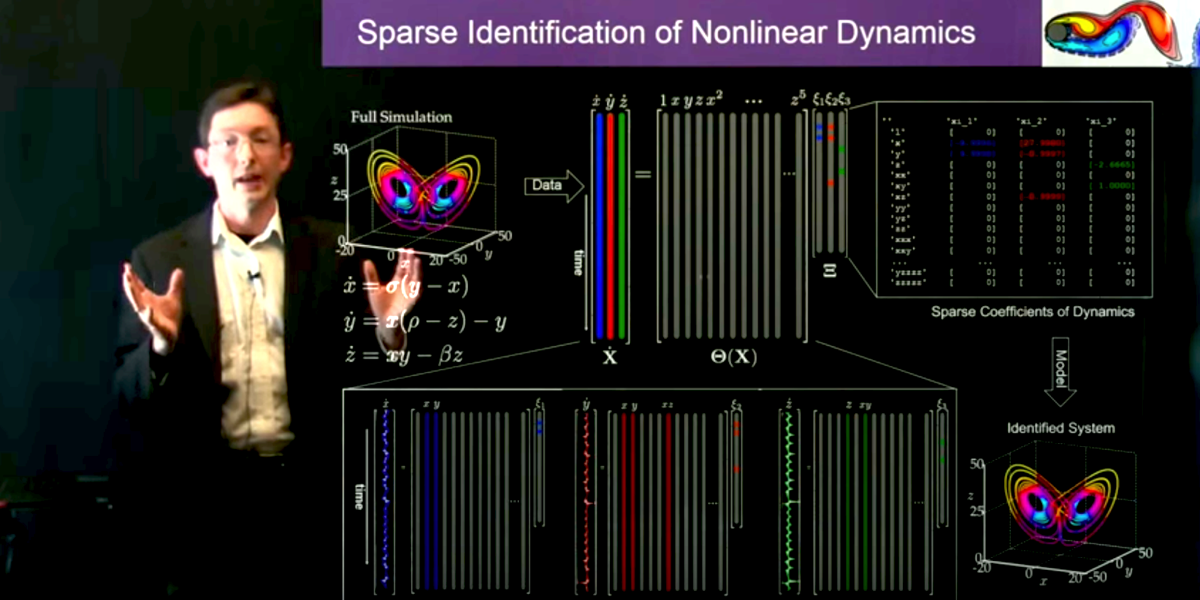
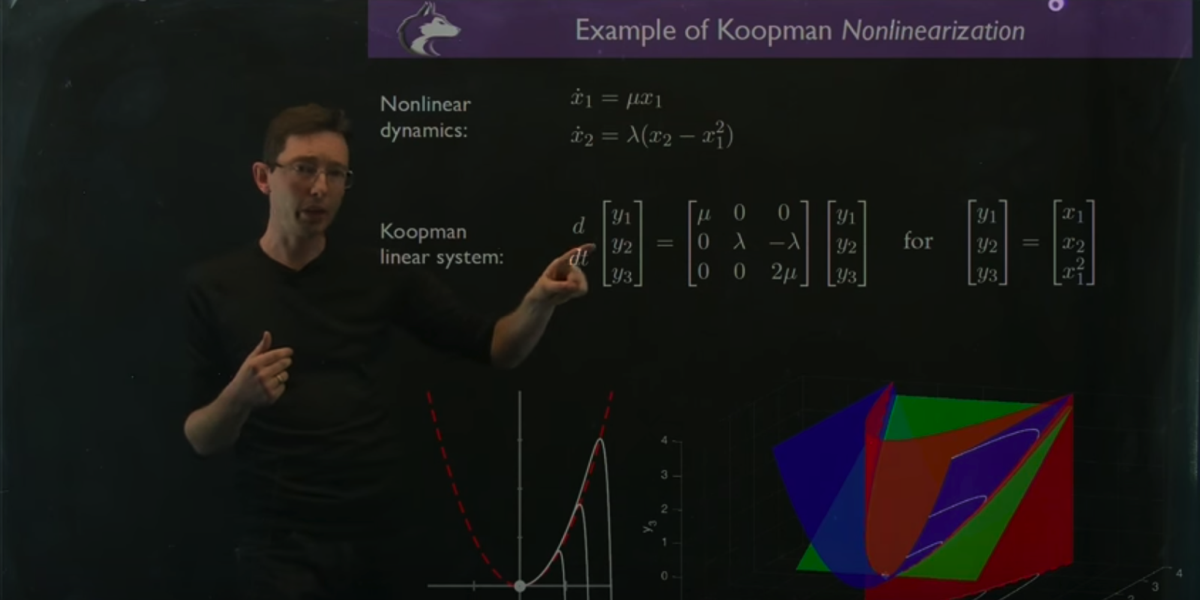
Dynamical systems provide a mathematical framework to describe the world around us, modeling the rich interactions between quantities that co-evolve in time. Formally, dynamical systems concerns the analysis, prediction, and understanding of the behavior of systems of differential equations or iterative mappings that describe the evolution of the state of a system. This formulation is general enough to encompass a staggering range of phenomena, including those observed in classical mechanical systems, electrical circuits, turbulent fluids, climate science, finance, ecology, social systems, neuroscience, epidemiology, and nearly every other system that evolves in time.
This chapter presents a modern perspective on dynamical systems in the context of current goals and open challenges. Data-driven dynamical systems is a rapidly evolving field, and therefore, we focus on a mix of established and emerging methods that are driving current developments. In particular, we will focus on the key challenges of discovering dynamics from data and finding data-driven representations that make nonlinear systems amenable to linear analysis.
Youtube playlist: Data-Driven Dynamical Systems
This chapter presents a modern perspective on dynamical systems in the context of current goals and open challenges. Data-driven dynamical systems is a rapidly evolving field, and therefore, we focus on a mix of established and emerging methods that are driving current developments. In particular, we will focus on the key challenges of discovering dynamics from data and finding data-driven representations that make nonlinear systems amenable to linear analysis.
Youtube playlist: Data-Driven Dynamical Systems