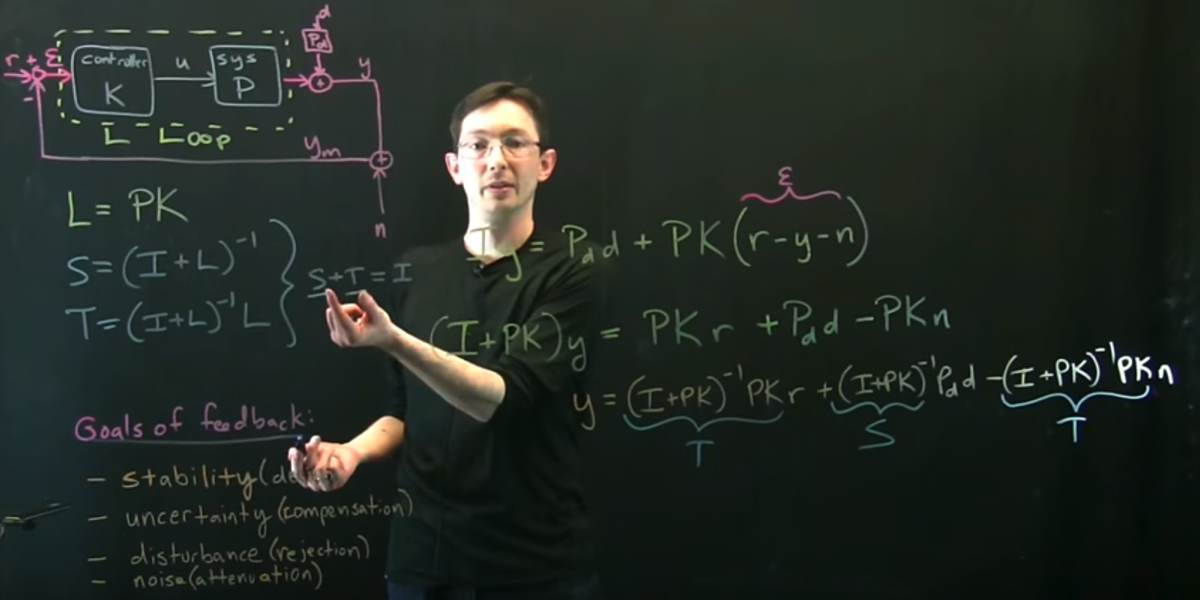The focus of this book has largely been on characterizing complex systems through dimensionality reduction, sparse sampling, and dynamical systems modeling. However, an overarching goal for many systems is the ability to actively manipulate their behavior for a given engineering objective. The study and practice of manipulating dynamical systems is broadly known as control theory, and it is one of the most successful fields at the interface of applied mathematics and practical engineering. Control theory is inseparable from data science, as it relies on sensor measurements (data) obtained from a system to achieve a given objective. In fact, control theory deals with living data, as successful application modifies the dynamics of the system, thus changing the characteristics of the measurements. Control theory forces the reader to confront reality, as simplifying assumptions and model approximations are tested.
Control theory has helped shape the modern technological and industrial landscape. Examples abound, including cruise control in automobiles, position control in construction equipment, fly-by-wire autopilots in aircraft, industrial automation, packet routing in the internet, commercial heating ventilation and cooling systems, stabilization of rockets, and PID temperature and pressure control in modern espresso machines, to name only a few of the many applications. In the future, control will be increasingly applied to high-dimensional, strongly nonlinear and multiscale problems, such as turbulence, neuroscience, finance, epidemiology, autonomous robots, and self driving cars. In these future applications, data-driven modeling and control will be vitally important; this is be the subject of Chapters 7 and10.
This chapter will introduce the key concepts from closed-loop feedback control. The goal is to build intuition for how and when to use feedback control, motivated by practical real-world challenges. Most of the theory will be developed for linear systems, where a wealth of powerful techniques exist. This theory will then be demonstrated on simple and intuitive examples, such as to develop a cruise controller for an automobile or stabilize an inverted pendulum on a moving cart.
Youtube playlist: Control Bootcamp
Control theory has helped shape the modern technological and industrial landscape. Examples abound, including cruise control in automobiles, position control in construction equipment, fly-by-wire autopilots in aircraft, industrial automation, packet routing in the internet, commercial heating ventilation and cooling systems, stabilization of rockets, and PID temperature and pressure control in modern espresso machines, to name only a few of the many applications. In the future, control will be increasingly applied to high-dimensional, strongly nonlinear and multiscale problems, such as turbulence, neuroscience, finance, epidemiology, autonomous robots, and self driving cars. In these future applications, data-driven modeling and control will be vitally important; this is be the subject of Chapters 7 and10.
This chapter will introduce the key concepts from closed-loop feedback control. The goal is to build intuition for how and when to use feedback control, motivated by practical real-world challenges. Most of the theory will be developed for linear systems, where a wealth of powerful techniques exist. This theory will then be demonstrated on simple and intuitive examples, such as to develop a cruise controller for an automobile or stabilize an inverted pendulum on a moving cart.
Youtube playlist: Control Bootcamp
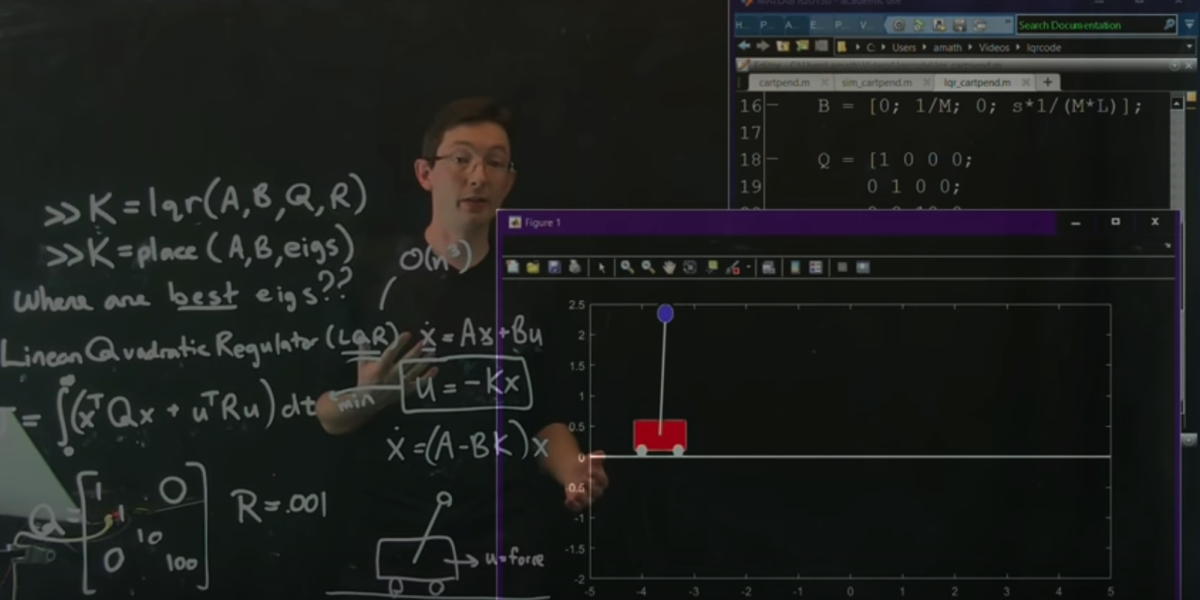
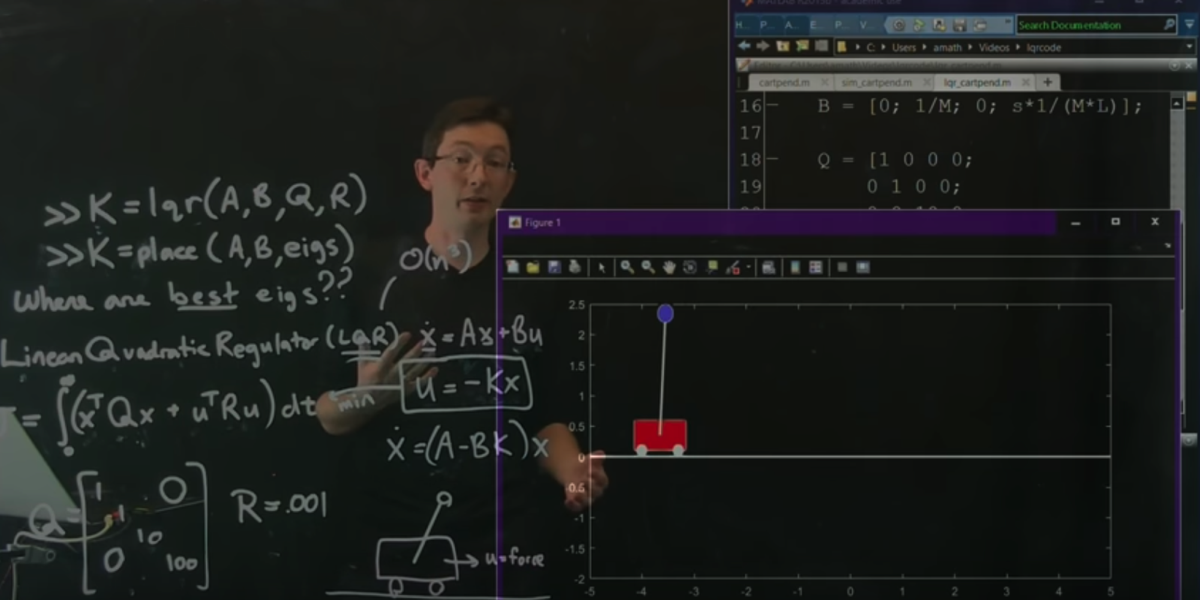
Section 8.3: Controllability
[ Controllability ] [ Part 2 ] [ Part 3 ] [ Part 4 ] [ Part 5 ] [ Part 6 ] [ Observability ]
Section 8.8: Robust control and frequency domain techniques
[Robustness ] [ Part 2 ] [ Part 3 ] [ Part 4 ]
[ Sensitivity ] [ Part 2 ]