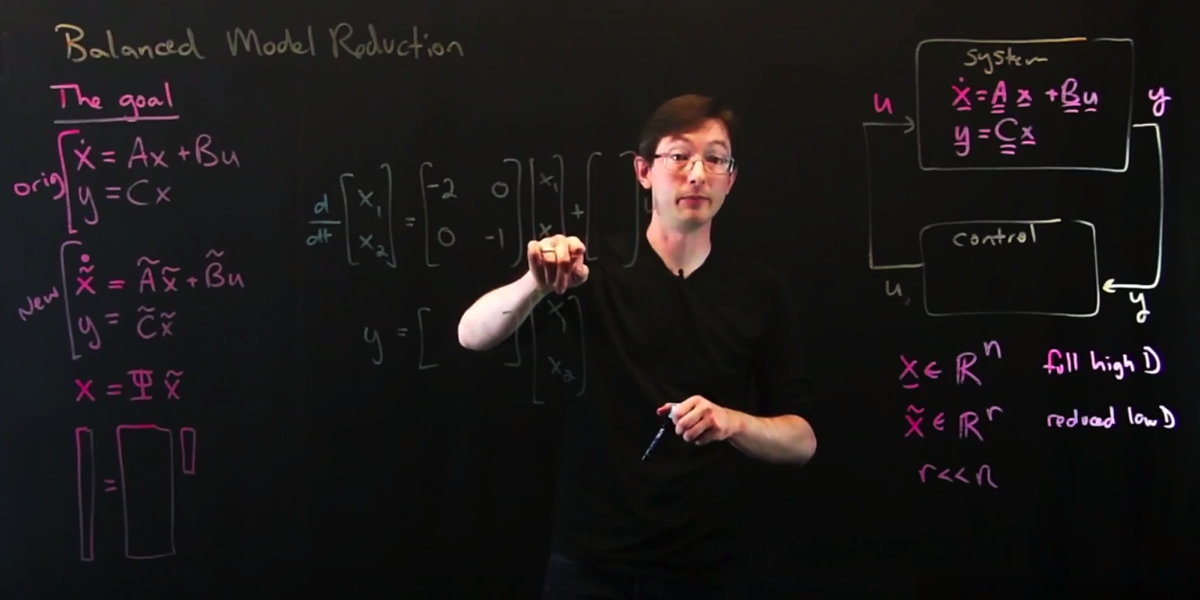Many systems of interest are exceedingly high dimensional, making them difficult to characterize. High-dimensionality also limits controller robustness due to significant computational time-delays. For example, for the governing equations of fluid dynamics, the resulting discretized equations may have millions or billions of degrees of freedom, making them expensive to simulate. Thus, significant effort has gone into obtaining reduced-order models that capture the most relevant mechanisms and are suitable for feedback control.
Here we will discuss a class of balanced reduced-order models that orders modes based on input--output energy. Thus, only modes that are both highly controllable and highly observable are selected, making balanced models ideal for control applications. In this chapter we also describe related procedures for model reduction and system identification, depending on whether or not the user starts with a high-fidelity model or simply has access to measurement data.
Youtube playlist: Data-Driven Control
Here we will discuss a class of balanced reduced-order models that orders modes based on input--output energy. Thus, only modes that are both highly controllable and highly observable are selected, making balanced models ideal for control applications. In this chapter we also describe related procedures for model reduction and system identification, depending on whether or not the user starts with a high-fidelity model or simply has access to measurement data.
Youtube playlist: Data-Driven Control