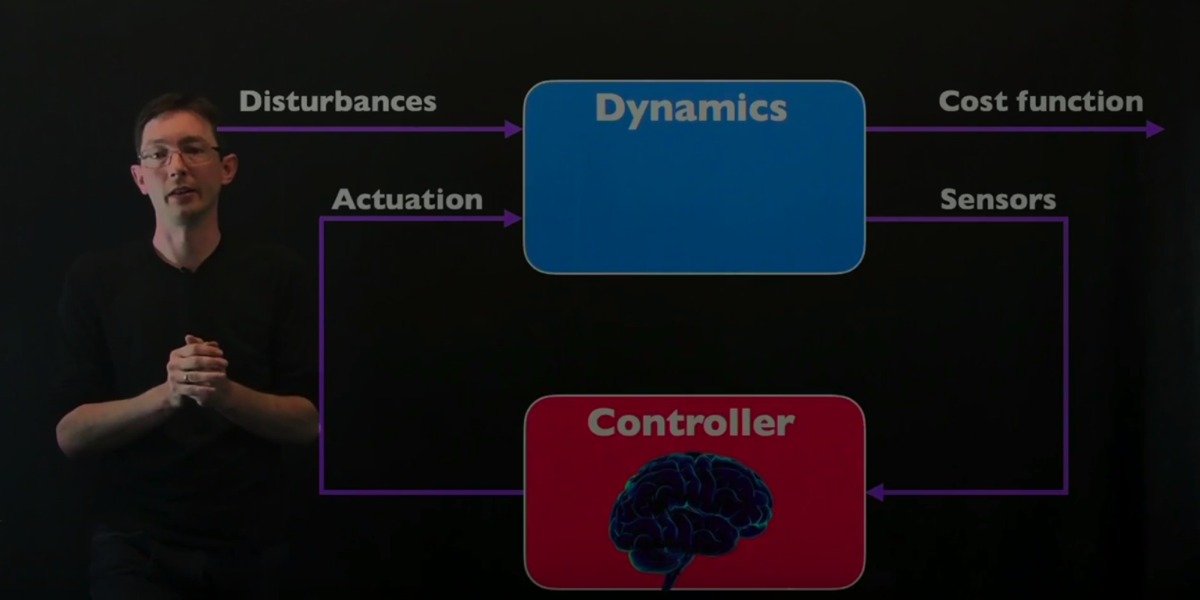
Control design often begins with a model of the system being controlled. Notable exceptions include model-free adaptive control strategies and many uses of PID control. For mechanical systems of moderate dimension, it may be possible to write down a model (e.g., based on the Newtonian, Lagrangian, or Hamiltonian formalism) and linearize the dynamics about a fixed point or periodic orbit. However, for modern systems of interest, as are found in neuroscience, turbulence, epidemiology, climate, and finance, typically there are no simple models suitable for control design.
Chapter 9 described techniques to obtain control-oriented reduced-order models for high-dimensional systems from data, but these approaches are limited to systems. Real-world systems are usually nonlinear and the control objective is not readily achieved via linear techniques. Nonlinear control can still be posed as an optimization problem with a high-dimensional, non-convex cost function landscape with multiple local minima. Machine learning is complementary, as it constitutes a growing set of techniques that may be broadly described as performing nonlinear optimization in a high-dimensional space from data. In this chapter we describe emerging techniques that use machine learning to characterize and control strongly nonlinear, high-dimensional, and multi-scale systems, leveraging the increasing availability of high-quality measurement data.
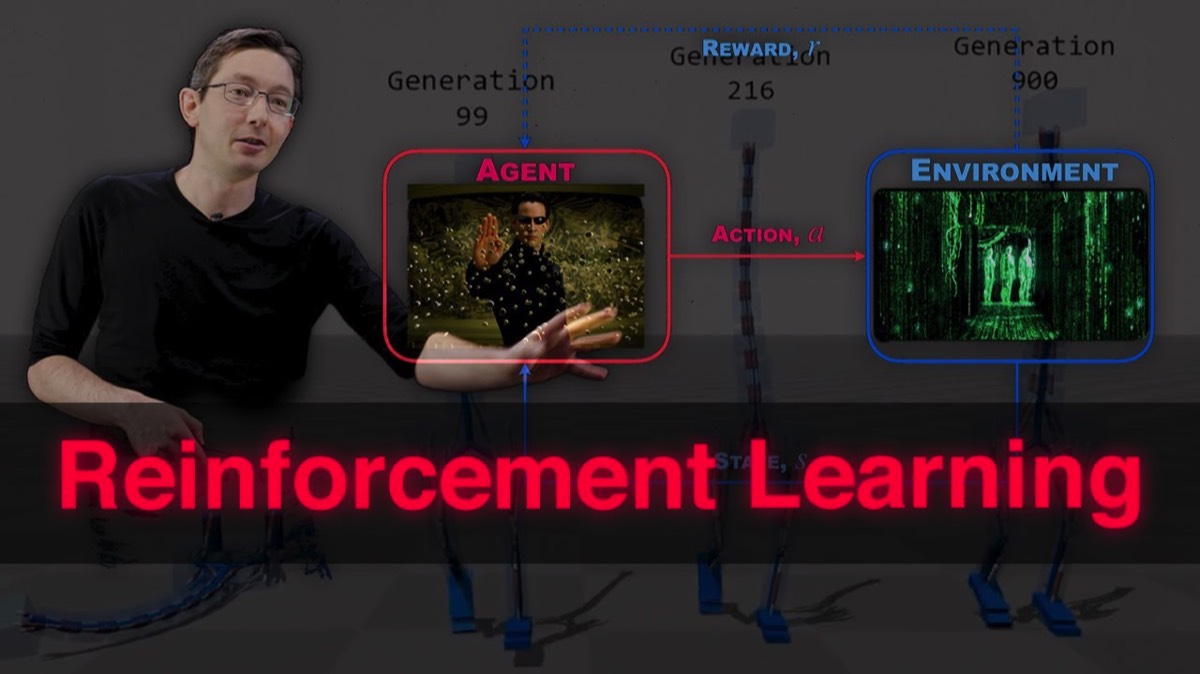
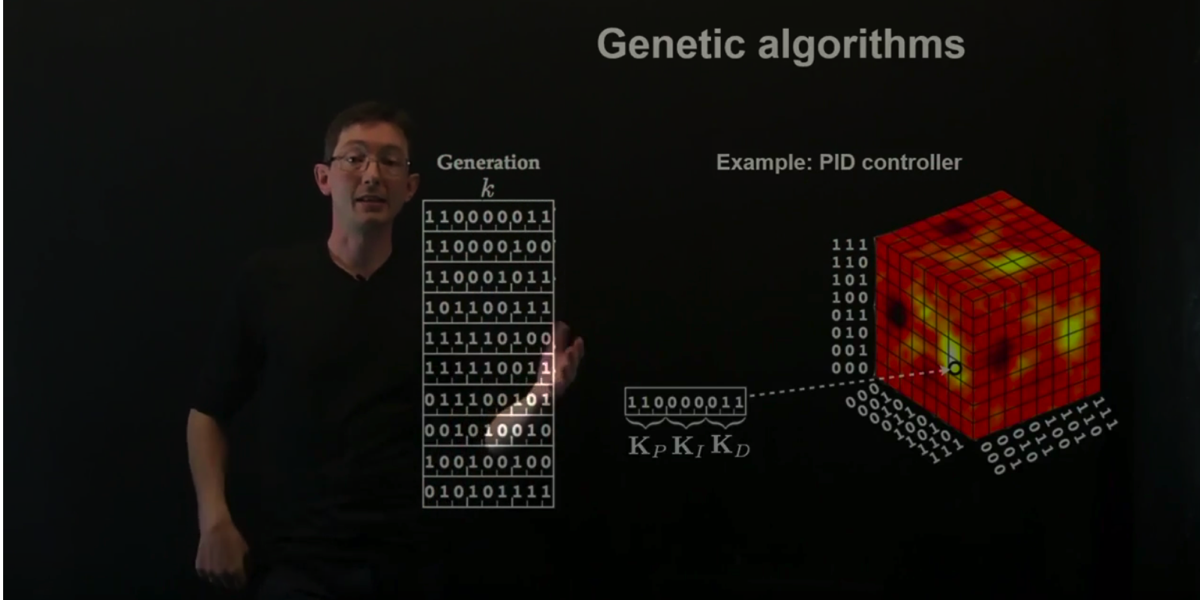
Broadly speaking, machine learning techniques may be used to 1) characterize a system for later use with model-based control, or 2) directly characterize a control law that effectively interacts with a system. This chapter will explore the use of machine learning to identify nonlinear input--output models for control and to directly identify controllers from input--output data. This is a rapidly developing field, with many powerful methods, such as reinforcement learning, iterative learning control, and genetic algorithms. Here we provide a high-level overview of these methods and then explore an example using genetic algorithms. We also describe the adaptive extremum-seeking control strategy, which optimizes the control signal based on how the system responds to perturbations.
Youtube playlist: Data-Driven Control
Chapter 9 described techniques to obtain control-oriented reduced-order models for high-dimensional systems from data, but these approaches are limited to systems. Real-world systems are usually nonlinear and the control objective is not readily achieved via linear techniques. Nonlinear control can still be posed as an optimization problem with a high-dimensional, non-convex cost function landscape with multiple local minima. Machine learning is complementary, as it constitutes a growing set of techniques that may be broadly described as performing nonlinear optimization in a high-dimensional space from data. In this chapter we describe emerging techniques that use machine learning to characterize and control strongly nonlinear, high-dimensional, and multi-scale systems, leveraging the increasing availability of high-quality measurement data.
Broadly speaking, machine learning techniques may be used to 1) characterize a system for later use with model-based control, or 2) directly characterize a control law that effectively interacts with a system. This chapter will explore the use of machine learning to identify nonlinear input--output models for control and to directly identify controllers from input--output data. This is a rapidly developing field, with many powerful methods, such as reinforcement learning, iterative learning control, and genetic algorithms. Here we provide a high-level overview of these methods and then explore an example using genetic algorithms. We also describe the adaptive extremum-seeking control strategy, which optimizes the control signal based on how the system responds to perturbations.
Youtube playlist: Data-Driven Control
Section 10.1: Nonlinear system identification for control
[ DMD w/ control ] [ DMDc example ] [ Koopman w/ control ] [ Part 2 ]
[ MPC ] [ SINDy w/ control ] [ SINDy+MPC ]
Section 10.2: Machine learning control
[ Video ]
[ Genetic algorithms ] [ GA+PID ] [ GA+PID Part 2 ] [ Genetic programming ] [ Genetic programming control ]
Section 10.3: Extremum-seeking control
[ Overview ] [ Matlab ] [ Simulink ] [ Challenging Example ] [ Applications ]