Neural networks (NNs) were inspired by the Nobel prize winning work of Hubel and Wiesel on the primary visual cortex of cats. Their seminal experiments showed that neuronal networks were organized in hierarchical layers of cells for processing visual stimulus. The first mathematical model of the NN, termed the Neocognitron in 1980, had many of the characteristic features of today’s deep convolutional NNs (or DCNNs), including a multi-layer structure, convolution, max pooling and nonlinear dynamical nodes. The recent success of DCNNs in computer vision has been enabled by two critical components: (i) the continued growth of computational power, and (ii) exceptionally large labeled data sets which take advantage of the power of a deep multi-layer architecture. Indeed, although the theoretical inception of NNs has an almost four-decade history, the analysis of the ImageNet data set in 2012 provided a watershed moment for NNs and deep learning, transforming the field of computer vision by dominating the performance metrics in almost every meaningful computer vision task intended for classification and identification. They are now being broadly applied across the engineering and physical sciences.
Supplementary Videos
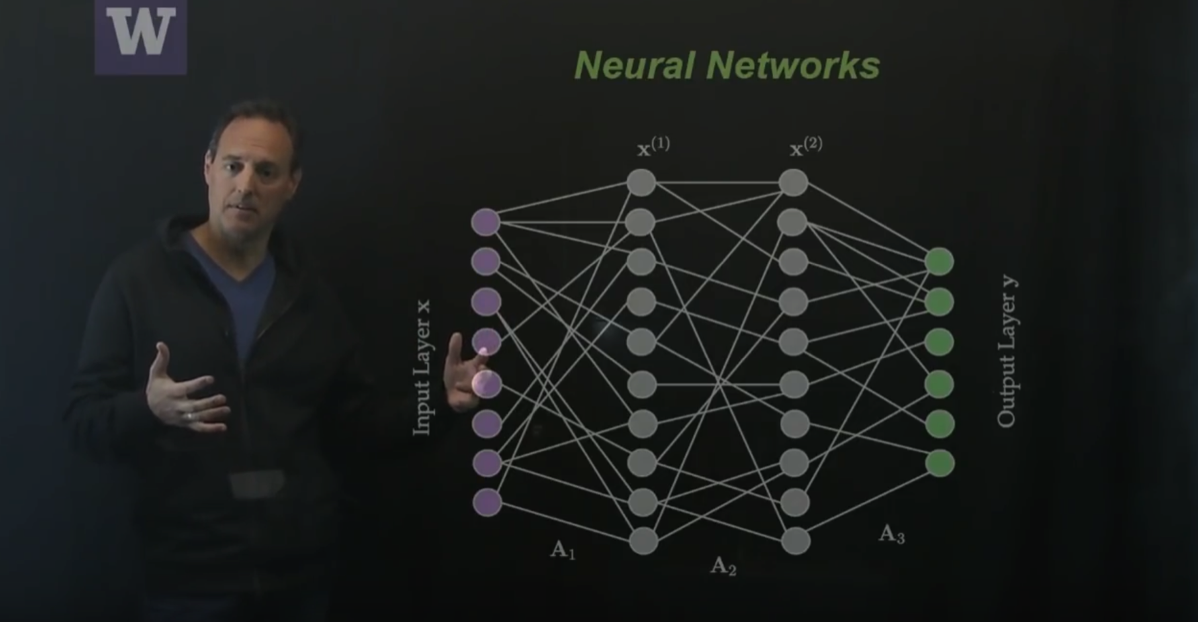
This video highlights some of the basic ideas of building neural networks [ View ]
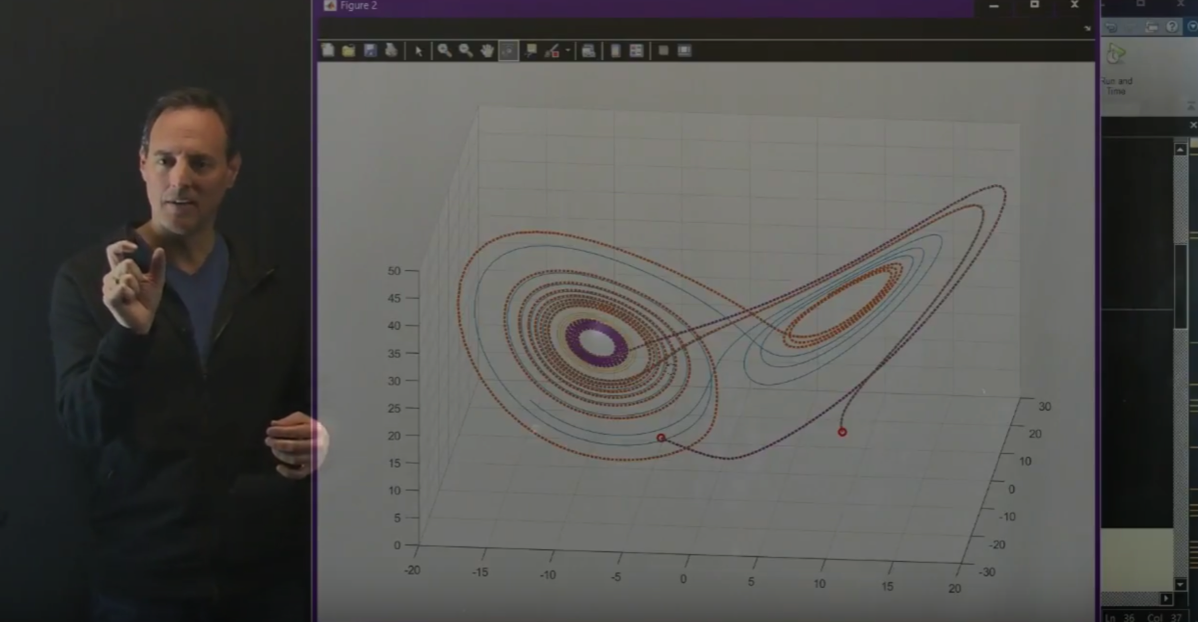
This video highlights how to train a neural network to learn time-stepping algorithms for dynamical systems [ View ]






